![]()
|
|
|---|
[Meßbedingungen] - [Durchführung] - [Laufzeiten] - [Graphiken] - [Detaillierte Resultate] - [Bemerkungen]
![]()
Datum: 07/02/2001
Ausgeführt von: Jasper Möller, moellerj@fmi.uni-konstanz.de
Betriebssystem: Linux 2.2.18
CPU: AMD Athlon, 800MHz
Speicher: 256MB
JDK: 1.3.0, IBM
Javaopt: -Xmx180M
Javacopt: -O
Datendatei: zufallszahlen/random.xxx
Für die Messung wird eine Datei mit vorgegebener Anzahl an Zufallszahlen eingelesen. Die Zufallszahlen werden in die PriorityQueue mit insert() eingefügt und danach wieder mit extractMin() ausgelesen (damit wird der Datensatz sortiert). Dies wird für jede Queue fünfmal wiederholt.
public static void main(...)
{
...
//Datei einlesen
long duration = 0;
int[] zufallszahlen;
//Die ersten zehn Knoten im Graphen
...
duration = System.currentTimeMillis();
for(int i = 0; i < zufallszahlen.length; ++i)
Queue.insert(zufallszahlen[i]);
while(!Queue.isEmpty())
Queue.extractMin();
duration = System.currentTimeMillis() - duration;
...
}Da die Ergebnisse der BucketQueues sich nur minimal von denen der normalen Queues unterscheiden, sind hier nur die Ergebnisse für die normalen Queues aufgeführt. Die Ergebnisse für die BucketQueues können dem Archiv entnommen werden.
|
|
BinomialHeapPQ |
FibonacciHeapPQ |
HeapPQ (d=2) |
WeakHeapPQ |
|---|---|---|---|---|
|
500 Zahlen |
215ms |
179ms |
78ms |
754ms |
|
1000 Zahlen |
204ms |
120ms |
72ms |
369ms |
|
1500 Zahlen |
215ms |
179ms |
78ms |
754ms |
|
2000 Zahlen |
241ms |
280ms |
89ms |
1306ms |
|
2500 Zahlen |
242ms |
428ms |
104ms |
2019ms |
|
3000 Zahlen |
264ms |
651ms |
110ms |
2894ms |
|
3500 Zahlen |
275ms |
843ms |
134ms |
4105ms |
|
4000 Zahlen |
298ms |
1164ms |
120ms |
5523ms |
|
4500 Zahlen |
297ms |
1417ms |
135ms |
7035ms |
|
5000 Zahlen |
317ms |
1826ms |
140ms |
8772ms |
|
5500 Zahlen |
340ms |
2368ms |
137ms |
10890ms |
|
6000 Zahlen |
343ms |
2155ms |
153ms |
13048ms |
|
6500 Zahlen |
364ms |
2667ms |
158ms |
15670ms |
|
7000 Zahlen |
369ms |
3026ms |
154ms |
18612ms |
|
7500 Zahlen |
379ms |
3653ms |
169ms |
22064ms |
|
8000 Zahlen |
402ms |
4219ms |
165ms |
25424ms |
|
8500 Zahlen |
402ms |
4645ms |
173ms |
28305ms |
|
9000 Zahlen |
414ms |
5544ms |
177ms |
32578ms |
|
9500 Zahlen |
429ms |
6354ms |
184ms |
37083ms |
|
10000 Zahlen |
462ms |
7247ms |
201ms |
43833ms |
|
|
LeftistTreePQ |
RedBlackTreePQ |
SortedListPQ |
UnsortedListPQ |
|---|---|---|---|---|
|
500 Zahlen |
42ms |
100ms |
57ms |
123ms |
|
1000 Zahlen |
40ms |
38ms |
41ms |
86ms |
|
1500 Zahlen |
42ms |
100ms |
57ms |
123ms |
|
2000 Zahlen |
44ms |
97ms |
85ms |
207ms |
|
2500 Zahlen |
47ms |
115ms |
136ms |
360ms |
|
3000 Zahlen |
50ms |
106ms |
185ms |
477ms |
|
3500 Zahlen |
52ms |
108ms |
250ms |
605ms |
|
4000 Zahlen |
54ms |
117ms |
346ms |
776ms |
|
4500 Zahlen |
56ms |
128ms |
449ms |
1102ms |
|
5000 Zahlen |
58ms |
112ms |
592ms |
1319ms |
|
5500 Zahlen |
61ms |
121ms |
763ms |
1634ms |
|
6000 Zahlen |
73ms |
125ms |
916ms |
2037ms |
|
6500 Zahlen |
67ms |
134ms |
1122ms |
2307ms |
|
7000 Zahlen |
69ms |
118ms |
1335ms |
2869ms |
|
7500 Zahlen |
70ms |
136ms |
1541ms |
2937ms |
|
8000 Zahlen |
73ms |
128ms |
1896ms |
3728ms |
|
8500 Zahlen |
76ms |
122ms |
2183ms |
4141ms |
|
9000 Zahlen |
79ms |
133ms |
2574ms |
4835ms |
|
9500 Zahlen |
82ms |
124ms |
2947ms |
5404ms |
|
10000 Zahlen |
85ms |
136ms |
3618ms |
6132ms |
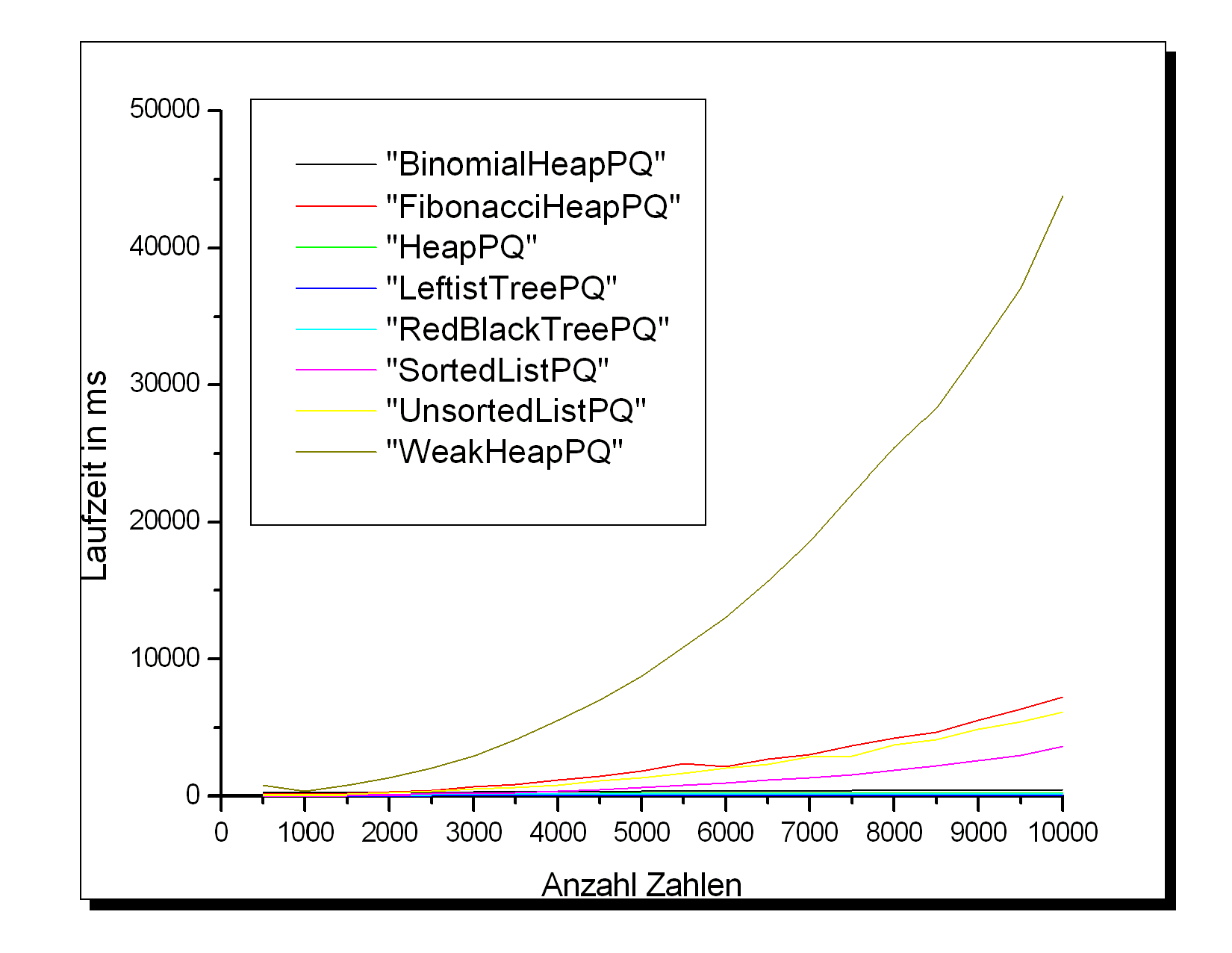
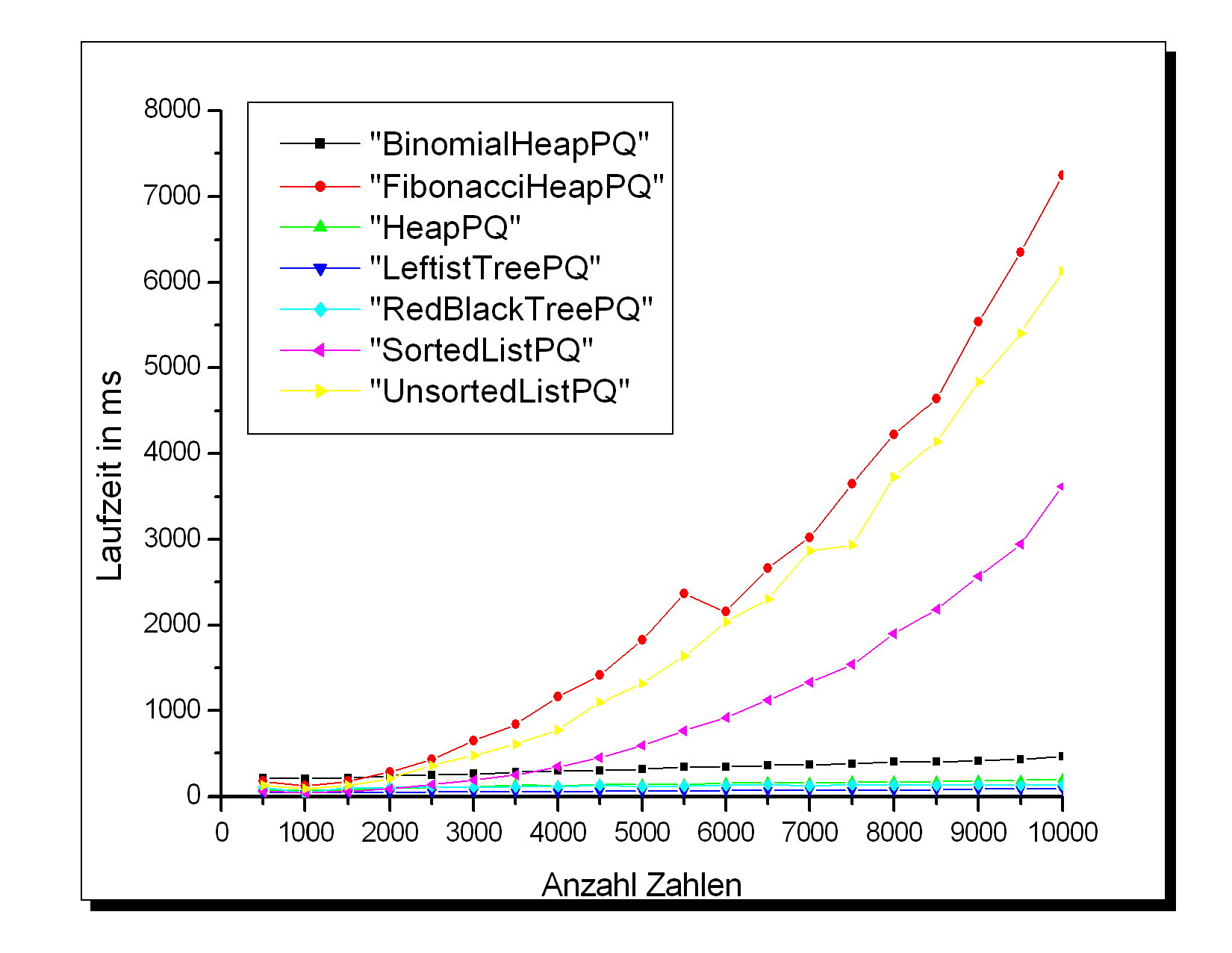
Detaillierte Resultate im Archiv: Zufallszahlen-Results.tar.gz
Bei dieser Applikation erweisen sich die mäßig komplexen Queues LeftistTreePQ, HeapPQ und RedBlackTreePQ als deutlich am effizientesten. Die auf decreaseKey()-Operationen optimierten Queues schneiden hier relativ schlecht ab, da diese Operation hier nicht gemessen wird und die anderen Operationen eher weniger effektiv implementiert weerden können. Auch die einfachen verlinkten Listen erweisen sich als für große Datensätze ungeeignet. Bei kleinen Datenmengen (bis ca. 2000 Zahlen) sind dagegen alle diese Queues in etwa gleich gut geeignet. Die hohen Werte für den WeakHeap dürften wieder an der nicht optimalen Implementation dieser Datenstruktur liegen.
![]()
|
|
|---|
[Meßbedingungen] - [Durchführung] - [Laufzeiten] - [Graphiken] - [Detaillierte Resultate] - [Bemerkungen]