![]()
[Meßbedingungen] - [Durchführung] - [Laufzeiten] - [Graphiken] - [Detaillierte Resultate] - [Bemerkungen]
![]()
Datum: 06-07/02/2001
Ausgeführt von: Jasper Möller, moellerj@fmi.uni-konstanz.de
Betriebssystem: Linux 2.2.18
CPU: AMD Athlon, 800MHz
Speicher: 256MB
JDK: 1.3.0, IBM
Javaopt: -Xmx180M
Javacopt: -O
Datendatei: graphen/zufallsgraphxxxx
Für die Messung wird jede Datei, die einen Graphen enthält, der Reihe nach geöffnet, der Graph eingelesen und danach die jeweils die kürzesten Wege von den ersten zehn Knoten im Graphen zu allen anderen bestimmt (single-source-shortest-path Problem). Gemessen wird die gesamte benötigte Laufzeit, um von diesen Knoten aus alle kürzesten Wege zu finden. Es gibt zwei Sorten von Graphen: Zufalls- und Exponentialgraph. Dies wird für jede Queue fünfmal wiederholt.
public static void main(...)
{
...
//Graph einlesen
long duration = 0;
Vertex[] array;
//Die ersten zehn Knoten im Graphen
...
duration = System.currentTimeMillis();
//Suche alle kürzsten Wege von allen 10 Startknoten aus
run(queue, graph, array)
duration = System.currentTimeMillis() - duration;
...
}Da die Ergebnisse der BucketQueues sich nur minimal von denen der normalen Queues unterscheiden, sind hier nur die Ergebnisse für die normalen Queues aufgeführt. Die Ergebnisse für die BucketQueues können dem Archiv entnommen werden.
|
|
BinomialHeapPQ |
FibonacciHeapPQ |
HeapPQ (d=2) |
WeakHeapPQ |
|---|---|---|---|---|
|
50 Knoten |
0,329s |
0,234s |
0,246s |
0,271s |
|
100 Knoten |
0,470s |
0,284s |
0,313s |
0,426s |
|
150 Knoten |
0,637s |
0,438s |
0,469s |
0,673s |
|
200 Knoten |
0,886s |
0,746s |
0,704s |
1,071s |
|
250 Knoten |
1,497s |
1,248s |
1,213s |
1,864s |
|
300 Knoten |
1,932s |
1,702s |
1,704s |
2,552s |
|
350 Knoten |
2,495s |
2,384s |
2,200s |
3,468s |
|
400 Knoten |
3,251s |
2,985s |
2,932s |
4,588s |
|
450 Knoten |
4,115s |
3,980s |
3,563s |
5,804s |
|
500 Knoten |
4,927s |
4,657s |
4,621s |
7,533s |
|
550 Knoten |
5,745s |
5,607s |
4,986s |
8,744s |
|
600 Knoten |
6,129s |
6,105s |
6,932s |
9,574s |
|
650 Knoten |
7,880s |
7,985s |
7,387s |
12,638s |
|
700 Knoten |
9,110s |
9,573s |
7,989s |
14,798s |
|
750 Knoten |
9,851s |
10,266s |
9,470s |
16,763s |
|
800 Knoten |
10,345s |
10,246s |
10,853s |
20,064s |
|
850 Knoten |
12,955s |
12,928s |
12,530s |
23,252s |
|
900 Knoten |
13,431s |
13,314s |
13,550s |
24,255s |
|
950 Knoten |
17,857s |
18,076s |
16,538s |
30,616s |
|
1000 Knoten |
19,094s |
19,250s |
17,353s |
30,732s |
|
|
LeftistTreePQ |
RedBlackTreePQ |
SortedListPQ |
UnsortedListPQ |
|---|---|---|---|---|
|
50 Knoten |
0,211s |
0,215s |
0,219s |
0,193s |
|
100 Knoten |
0,303s |
0,375s |
0,298s |
0,300s |
|
150 Knoten |
0,468s |
0,562s |
0,440s |
0,425s |
|
200 Knoten |
0,678s |
0,772s |
0,680s |
0,664s |
|
250 Knoten |
1,238s |
1,333s |
1,257s |
1,205s |
|
300 Knoten |
1,779s |
1,848s |
1,746s |
1,846s |
|
350 Knoten |
2,174s |
2,294s |
2,299s |
2,280s |
|
400 Knoten |
2,898s |
3,186s |
3,034s |
3,119s |
|
450 Knoten |
3,860s |
4,067s |
3,942s |
4,053s |
|
500 Knoten |
4,639s |
4,747s |
4,538s |
5,049s |
|
550 Knoten |
5,666s |
5,555s |
5,626s |
5,610s |
|
600 Knoten |
5,759s |
6,025s |
6,237s |
6,273s |
|
650 Knoten |
6,992s |
7,326s |
8,101s |
7,675s |
|
700 Knoten |
8,159s |
8,115s |
8,639s |
8,720s |
|
750 Knoten |
9,626s |
9,554s |
10,377s |
10,253s |
|
800 Knoten |
10,057s |
9,991s |
10,744s |
10,785s |
|
850 Knoten |
11,862s |
14,486s |
12,815s |
13,083s |
|
900 Knoten |
13,189s |
12,948s |
13,764s |
13,831s |
|
950 Knoten |
17,208s |
17,519s |
18,685s |
19,243s |
|
1000 Knoten |
22,097s |
18,953s |
20,856s |
20,756s |
|
|
BinomialHeapPQ |
FibonacciHeapPQ |
HeapPQ (d=2) |
WeakHeapPQ |
|---|---|---|---|---|
|
50 Knoten |
0,220s |
0,159s |
0,151s |
0,177s |
|
103 Knoten |
0,349s |
0,198s |
0,213s |
0,241s |
|
153 Knoten |
0,370s |
0,243s |
0,249s |
0,312s |
|
205 Knoten |
0,399s |
0,240s |
0,271s |
0,328s |
|
274 Knoten |
0,411s |
0,248s |
0,266s |
0,377s |
|
302 Knoten |
0,448s |
0,266s |
0,302s |
0,367s |
|
367 Knoten |
0,491s |
0,269s |
0,299s |
0,400s |
|
404 Knoten |
0,473s |
0,284s |
0,306s |
0,450s |
|
490 Knoten |
0,511s |
0,314s |
0,330s |
0,530s |
|
540 Knoten |
0,560s |
0,383s |
0,458s |
0,563s |
|
595 Knoten |
0,559s |
0,362s |
0,385s |
0,612s |
|
655 Knoten |
0,627s |
0,414s |
0,407s |
0,702s |
|
721 Knoten |
0,642s |
0,447s |
0,429s |
0,806s |
|
794 Knoten |
0,663s |
0,487s |
0,451s |
0,897s |
|
874 Knoten |
0,724s |
0,543s |
0,496s |
1,009s |
|
962 Knoten |
0,858s |
0,625s |
0,583s |
1,170s |
|
1059 Knoten |
0,771s |
0,647s |
0,537s |
1,239s |
|
1165 Knoten |
0,828s |
0,766s |
0,603s |
1,522s |
|
1282 Knoten |
0,952s |
0,886s |
0,703s |
1,687s |
|
1411 Knoten |
0,997s |
1,021s |
0,758s |
1,977s |
|
1553 Knoten |
1,158s |
1,204s |
0,852s |
2,300s |
|
1709 Knoten |
1,337s |
1,448s |
0,991s |
2,902s |
|
1880 Knoten |
1,342s |
1,438s |
1,083s |
3,066s |
|
2069 Knoten |
1,483s |
1,898s |
1,181s |
3,931s |
|
|
LeftistTreePQ |
RedBlackTreePQ |
SortedListPQ |
UnsortedListPQ |
|---|---|---|---|---|
|
50 Knoten |
0,139s |
0,134s |
0,147s |
0,135s |
|
103 Knoten |
0,204s |
0,195s |
0,197s |
0,180s |
|
153 Knoten |
0,221s |
0,278s |
0,219s |
0,211s |
|
205 Knoten |
0,237s |
0,304s |
0,267s |
0,213s |
|
274 Knoten |
0,249s |
0,323s |
0,244s |
0,230s |
|
302 Knoten |
0,266s |
0,381s |
0,243s |
0,261s |
|
367 Knoten |
0,269s |
0,339s |
0,242s |
0,256s |
|
404 Knoten |
0,275s |
0,350s |
0,273s |
0,269s |
|
490 Knoten |
0,313s |
0,377s |
0,309s |
0,306s |
|
540 Knoten |
0,354s |
0,395s |
0,311s |
0,360s |
|
595 Knoten |
0,322s |
0,427s |
0,332s |
0,390s |
|
655 Knoten |
0,368s |
0,440s |
0,386s |
0,444s |
|
721 Knoten |
0,386s |
0,456s |
0,378s |
0,482s |
|
794 Knoten |
0,397s |
0,481s |
0,443s |
0,511s |
|
874 Knoten |
0,501s |
0,521s |
0,471s |
0,583s |
|
962 Knoten |
0,503s |
0,570s |
0,503s |
0,669s |
|
1059 Knoten |
0,498s |
0,581s |
0,514s |
0,707s |
|
1165 Knoten |
0,542s |
0,603s |
0,592s |
0,806s |
|
1282 Knoten |
0,621s |
0,709s |
0,678s |
0,941s |
|
1411 Knoten |
0,633s |
0,746s |
0,686s |
1,040s |
|
1553 Knoten |
0,776s |
0,909s |
0,892s |
1,285s |
|
1709 Knoten |
0,845s |
1,037s |
1,067s |
1,560s |
|
1880 Knoten |
1,006s |
1,122s |
1,067s |
1,601s |
|
2069 Knoten |
1,028s |
1,419s |
1,322s |
1,982s |
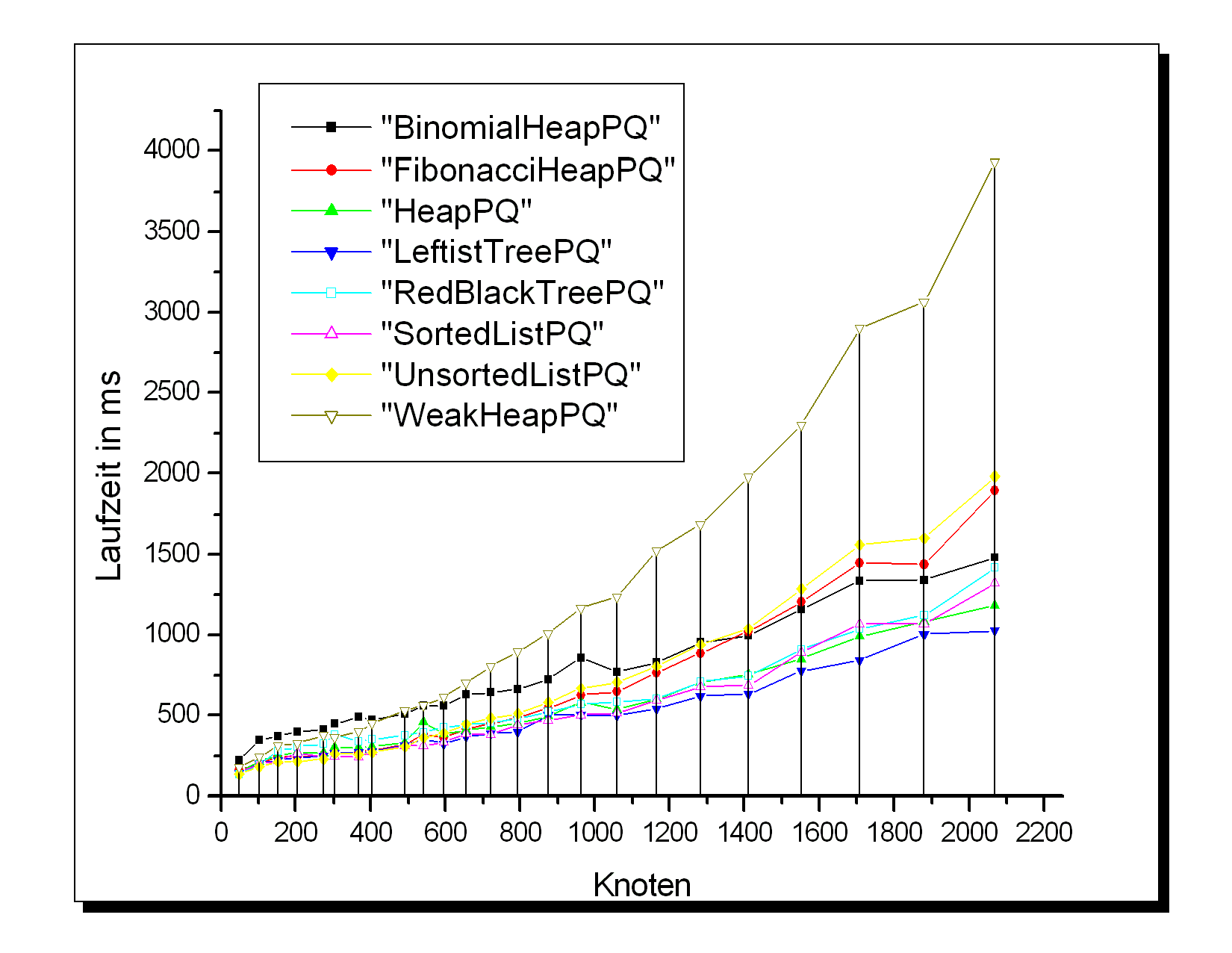
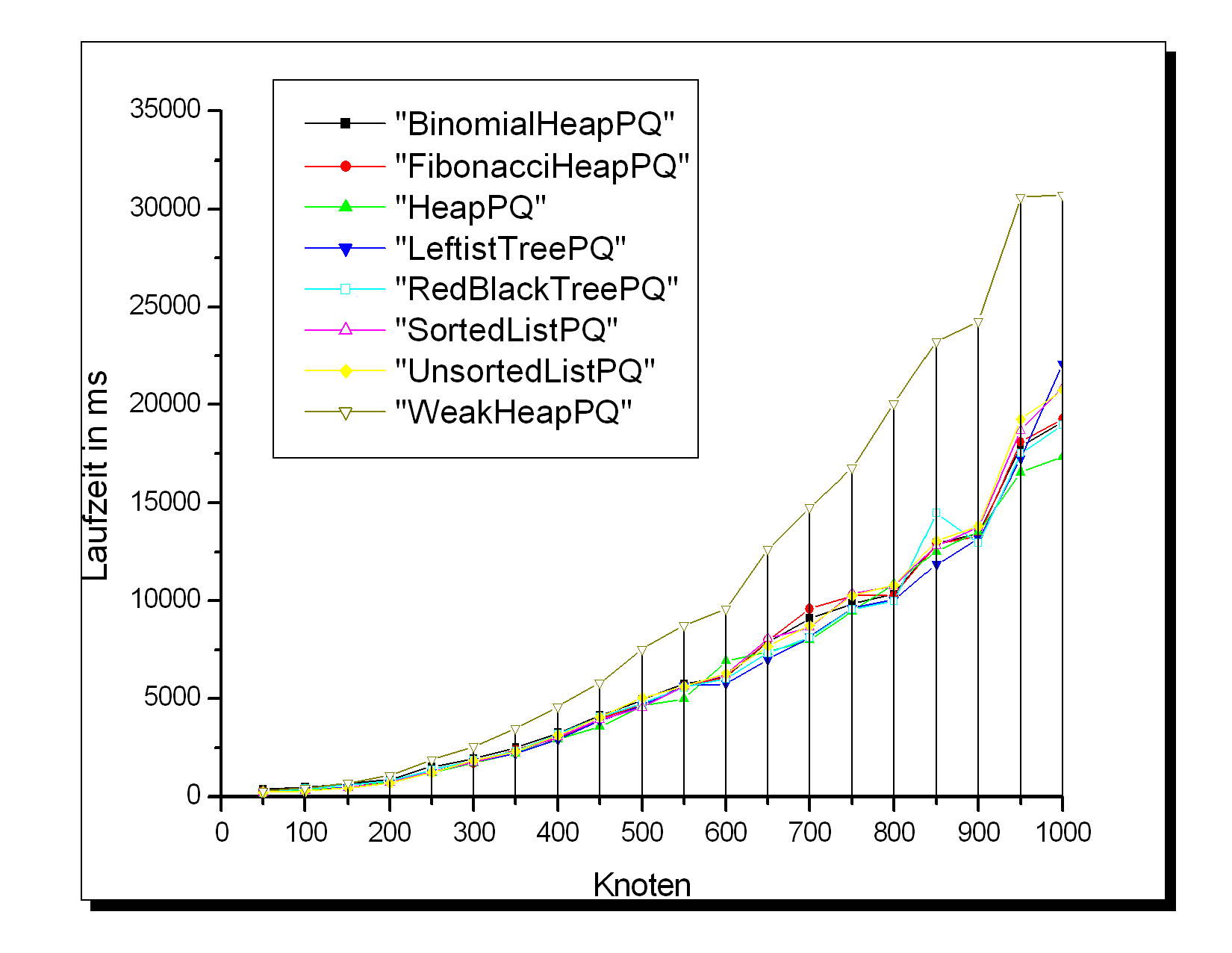
Detaillierte Resultate im Archiv: Zufallsgraph-Results.tar.gz
Bei dieser Applikation liegen bis auf die WeakHeapPQ (verursacht durch ineffiziente Implementierung) alle PriorityQueues sehr dicht beieinander. Lediglich bei großen Exponentialgraphen erweist sich die LeftistTreePQ als etwas effizienter als der Rest, gefolgt von HeapPQ, SortedListPQ und RedBlackTreePQ. Es ist nicht klar erkennbar, ob die auf decreaseKey() optimierten Queues ihren sonst vorhanden Overhead durch eine besonders schnelle Implementation von decreaseKey() ausgleichen können, oder ob es sich hierbei um die üblichen Meßfehler handelt - immerhin liegt die höchste Laufzeit bei nur ca. 20 Sekunden für die größten Graphen.
![]()
[Meßbedingungen] - [Durchführung] - [Laufzeiten] - [Graphiken] - [Detaillierte Resultate] - [Bemerkungen]